Р. Вишневский

Обобщенный закон гравитации

Теоретические модели «Великого объединения» фундаментальных взаимодействий преследуют, в конечном счете, цель: связать закон всемирного тяготения Ньютона и классические уравнения электродинамики в единую теорию света и вещества.

Возможным основанием для подобного объединения может служить обобщенный закон гравитации, излагаемый в настоящей статье.

Сила притяжения между двумя точечными материальными телами с массами т₁ и т₂, находящимися на расстоянии r друг от друга, выражается законом Ньютона:

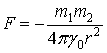(1)

Это т.н. рационализованная форма закона; здесь g₀ – абсолютная гравитационная, равная:

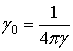g = 6,6720×10^-11 Нм²кг^-2 – гравитационная постоянная. (Все выражения и единицы физических величин здесь и далее приведены в системе СИ).

Законы движения планет Солнечной системы Кеплера, на основании которых был сформулирован закон (1), содержат в себе основание для столь же фундаментального закона природы: о всемирной ротации тел. Именно так следует понимать третий закон Кеплера, выражающий значение модуля индукции ротационного (R) поля Солнца на расстоянии r:

W_u²

(2)

m_u

4pg₀r³

где m_u – масса Солнца; g₀– абсолютная гравитационная. Вектор индукции Солнца W_uявляется силовой характеристикой R-поля, которое вращает планету вокруг светила. Как следует из выражения (2), модуль индукции – величина, характеризующая внутренние свойства Солнца, проявляющиеся на расстоянии r. При этом численное значение угловой скорости обращения планеты совпадает с физической величиной W_u, что и послужило причиной замены силы R-поля на переносную силу инерции планеты.

Законы тяготения (1) и ротации (2), дополняя друг друга, создают полное описание силового воздействия гравиротационного (GR) поля Солнца на планету. Один из них определяет силовую характеристику G-поля (напряженность G), второй – выражает силовую характеристику R-поля (индукция W). В результате воздействия GR-поля Солнца на планету массы т, суммарная сила выражается равенством:

F_u= – mG_u + m[VW_u],

где V – вектор скорости движения планеты. В стационарном состоянии GR-поля Солнца суммарная сила F_uравна нулю.

Гравиротационным полем обладают все материальные тела в природе, однако не все из них характеризуются абсолютной гравитационной g₀, поэтому представляет интерес обобщение законов (1) и (2) на тела с произвольной гравитационной постоянной g_*. Обобщенный закон ротации в таком случае имеет вид:

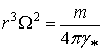. (3)

Правая часть этого равенства выражает гравитационную характеристику данной массы – поток напряженности G-поля, заключенный в единице телесного угла. Назовем эту физическую величину плотностью потока напряженности гравистатического поля и обозначим

= . (4)

Закон Кеплера предоставляет возможность выражения плотности потока данного тела, как с помощью его внутренних характеристик (т, g_*), так и с помощью параметров пробного тела, находящегося на орбите вокруг источника G-поля:

= r³W², (5)

где r – радиус орбиты пробного тела; W – угловая скорость вращения вокруг источника G-поля. Величину можно также определить по известному радиусу орбиты r и орбитальной скорости V пробного тела:

= rV². (6)

Этот способ определения широко применяется в астрономии для вычисления массы удаленных объектов из (4). В последнем случае роль пробного тела играет спутник объекта.

Выражения для плотности потока напряженности G-поля источника (4), (5) и (6) тождественны и используют либо внутренние (4), либо внешние (5), (6) проявления его гравитационной сущности.

С учетом равенства (4) обобщенный закон гравитации принимает форму:

₁

(7)

m₂

r²

где F – сила гравитационного воздействия плотности потока напряженности ₁ первого тела на массу т₂ второго; r – расстояние между телами. Замечательным свойством обобщенного закона гравитации (7) является его способность описывать взаимодействие материальных тел, имеющих различные гравитационные постоянные, а также взаимодействия, для которых гравитационная постоянная не установлена.

Используем это свойство закона (7) для описания взаимодействия микрочастиц в планетарной модели атома Бора.

Согласно правилу квантования орбит, электрон, движущийся по круговой основной орбите атома водорода, имеет момент импульса, равный (п = 1):

mV₁r₁ =, (8)

где m – масса покоя электрона; V₁– скорость электрона вдоль первой боровской орбиты; r₁– радиус этой орбиты; – постоянная Планка.

Гравитационная скорость электрона в атоме предполагает источник G-поля, расположенный в центре круговой орбиты – ядре атома. Сам электрон в данном случае можно рассматривать в качестве пробного тела, что позволяет определить плотность потока (6) напряженности G-поля ядра атома водорода с помощью параметров орбиты электрона. Для этого возведем в квадрат и разделим на r₁m² обе части равенства (8); в результате получим:

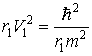Здесь левая часть равенства выражает плотность потока G-поля ядра атома ₀, численное значение которой составляет

₀ 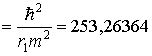м³/с², (9)

характеризуя внутренние гравитационные свойства стационарного источника, и остается неизменным при любых квантовых состояниях атома; оно не зависит от радиуса стационарной орбиты электрона.

Согласно обобщенному закону гравитации (7), сила воздействия протона на электрон в основном состоянии атома водорода:

F₁	=	₀ m	= 8,2388578×10^-8 Н.
		²

Энергия связи электрона с ядром при этом составляет

U₁	=	₀ m	= – 4,3598145×10^-¹⁸ Дж;

кинетическая энергия электрона на первой боровской орбите

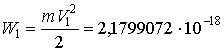Дж,

а полная энергия атома в основном состоянии

E₁ = U₁ + W₁ = –2,1799072×10^-18 Дж.

Приведенный расчет силовой и энергетических характеристик атома водорода показывает, что обобщенный закон гравитации (7) совместно с плотностью потока напряженности G-поля ₀ (9) допускает описание микромира.

Постоянная ₀проявляет все признаки фундаментальной константы. Это подтверждают следующие примеры.

1. Линейная скорость электрона на первой боровской орбите выражается через постоянные и _{0 :}

V₁	=	₀ m	.

2. Угловая скорость обращения электрона на той же орбите:

W₁	=	₀ m	.
		r₁

3. Т.н. энергия Ридберга выражается равенством:

Rу	=	₀² m³	.
		2²

4. Т.н. квант циркуляции соотносится с плотностью потока G-поля ядра атома _{0 :}

	=	₀	.
		V₁

5. Константа связи электромагнитного взаимодействия имеет форму:

₀ m	.
с₀

где с₀ – скорость света в вакууме.

6. Для сильного взаимодействия подобная константа выражается равенством:

₀ m_р	= 13,399041,
с₀

где m_р – масса покоя протона.

7. Выражение для константы связи слабого взаимодействия

₀ m_F	~ (1,02×10^-5)
с₀

позволяет установить численное значение массы покоя m_Fнекоторой «частицы Ферми». Константа связи гравитационного взаимодействия утрачивает смысл, т.к. все взаимодействия – гравитационные.

Можно показать, что для электрона в атоме водорода имеет место равенство:

2, (10)

где r₁ – радиус боровский первый; j₁(В)- потенциал ядра атома на расстоянии радиуса орбиты, выраженный в вольтах; r_е – радиус электрона классический; j_е(В)- собственный потенциал электрона на расстоянии r_е в вольтах. Если учесть, что между потенциалом и скоростью существует связь:

то левая часть равенства (10) известна: ₀, следовательно, плотность потока напряженности собственного G-поля электрона

_е = = ₀, (11)

откуда собственный гравитационный потенциал электрона

j_е	=	₀	= .
		r_е

Обобщенный закон ротации (3) справедлив для любой стационарной GR-системы, включая планетарную систему модели атома Бора. В основном состоянии атома этот закон в форме (5) имеет вид:

₀.

Кроме основной орбиты, имеется множество п таких орбит, что радиус п-ной

r_n = a_nr₁,

а угловая скорость электрона на п-ной орбите

W_n = W₁/b_n.

Если коэффициенты равны соответственно:

a_n = n² и b = n³,

где n = …

то выполняется равенство:

₀.

Число n в данном случае означает номер стационарной орбиты электрона в атоме водорода. При n = 1 орбита называется основной.

Энергия связи электрона с ядром атома на п-ной стационарной орбите выражается равенством

где множитель n означает, что величина действия кратна постоянной Планка. При переходах атома из одного стационарного состояния в другое, потенциальная энергия U_n изменяется. В частности, при переходах электрона с высшей орбиты m на более низкую n, излучается квант энергии; частота излучения равна

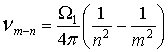что совпадает со спектром оптических излучательных переходов атома водорода.

Из формулы (4) по известной массе покоя электрона и плотности потока напряженности ₀можно вычислить значение гравитационной постоянной для электрона:

g_*	=	m	= ;
		4p₀

оно на 42 порядка меньше значения абсолютной гравитационной g₀, что говорит о количественном, но не качественном различии между планетарной системой модели атома Бора и Солнечной системой.

Если отвлечься от пространственно-временных различий между этими системами, то обе они представляют GR-системы. В стационарном состоянии подобной системы гравитационное и ротационное поля сосуществуют раздельно, но при возбуждении, G- и R-поля образуют единую вихревую систему нестационарного процесса.

Наглядным проявлением нестационарного процесса в GR-системе служит торнадо, циклон и другие вихревые образования в атмосфере.

Примером нестационарного процесса в GR-системе атома является его возбужденное состояние. Природа использовала это явление для создания т.н. аурического поля человека. Силовые воронки – чакры ауры позволяют наблюдать его проявление вне атома.

Аналогичные процессы происходят в космосе. Например, на фотографии явления «Cart wheel» хорошо различим вихревой характер GR-системы космического объекта.

Выводы:

1. Все материальные тела в природе представляют собой источники GR-поля.

2. Обобщенные законы гравитации и ротации тел применимы для описания взаимодействий микрочастиц методами классической физики, откуда следует: качественного различия между кулоновским и гравитационным полями нет.

3. Электродинамика, по существу, представляет собой специфическую форму доведенной до совершенства теории GR-поля микросистемы атома, которая отличается от Солнечной своими пространственно-временными характеристиками.

4. Основным законом динамики GR-системы может служить система уравнений Максвелла, адаптированная к GR-полю.

5. Одной из проблем при описании микромира с помощью обобщенного закона гравитации остается знаковая проблема «гравитационных зарядов».
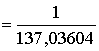