Р. Вишневский

Планетарно-вихревая модель атома

 

Принятое в физике квантомеханическое описание атома неполно, оно упускает из виду такое замечательное явление природы, как чакра.

Термин «чакра» заимствован из метафизической литературы и означает вихрь. Вихри ауры человека, наблюдаемые с помощью экстрасенсорного восприятия, обязаны своим происхождением нестационарным процессам в атомах вещества.

Явление чакры состоит в концентрации потока напряженности гравитационного поля возбужденного атома в узком конусе силового вихря. Статья посвящена описанию явления чакры в атоме водорода.

Основной недостаток классической электродинамики заключается в отсутствии связи между вектором скорости микрочастицы и потенциалом поля, в котором она движется. Частично этот вопрос решен  квантовой электродинамикой; она использует понятие скорости микрочастицы, введенное  де Бройлем. Его формула – чисто гравитационная система, так что квантовая электродинамика – некий симбиоз электромагнитной и гравитационной систем.

Полный переход от электромагнитной системы единиц физических величин к единицам абсолютной системы (кг-м-с) возможен путем приравнивания электрического заряда электрона его массе покоя:

е [Кл] = т [кг]                                                     (1)

При этом все соотношения между физическими величинами электродинамики остаются в силе. Например, закон Кулона принимает форму:

,

где m₁ и m₂ – массы покоя двух электронов, g_е – гравитационная постоянная пространства-времени электрона. Она значительно отличается от абсолютной гравитационной Солнечной системы, что, возможно, связано с различием скорости течения времени.

Трансформация единиц физических величин (1) позволяет ввести понятие модуля вектора скорости движения микрочастицы V:

,

где j - гравитационный потенциал поля, в котором движется электрон. Полученная в результате преобразования единиц система называется светодинамикой – теорией гравиротационного (GR) поля. Напряженность G гравитационного поля в этой системе имеет смысл ускорения, а индукция W ротационного поля имеет значение угловой скорости движения частицы. При этом обнаруживается, что электромагнетизм – это теория высоких гравитационных и угловых скоростей. В светодинамике действительны не только законы Ньютона, но и уравнения Максвелла, адаптированные к GR-полю. Далее в статье используются единицы и понятия светодинамики.

Описываемая в статье планетарно-вихревая модель атома дополняет модель Бора нестационарными процессами в атоме водорода при переходах его из одного стационарного состояния в другое.

В соответствии с правилом квантования, на орбите n-уровня электрон движется по круговой орбите радиуса r_n со скоростью V_n, его момент импульса равен:

          (n = 1, 2, 3, …),                          (2)

где m – масса покоя электрона,  - постоянная Планка, n – номер уровня. Любая стационарная орбита электрона может быть охарактеризована с помощью параметров первой боровской орбиты и числа n. Так, радиус n –орбиты:

,

где r₁ – радиус первый боровский (n =1).

 Модуль скорости электрона на n-орбите:

.

Здесь V₁ – модуль скорости движения электрона вдоль первой боровской орбиты. Частота обращения электрона вокруг ядра атома на n-уровне равна:

.                                                   (3)

Соответственно, угловая скорость движения электрона на n-орбите:

.                                                     (4)

Универсальная характеристика электрона – его внутренняя энергия на n-уровне:

,

где  U_n – потенциальная энергия электрона, T_n – его кинетическая энергия. Последняя определяется через модуль скорости:

.

Для установления значения потенциальной энергии электрона на n-уровне, умножим обе части равенства (2) на угловую скорость W_n (4):

или, с учетом (3):

В правой части последнего равенства находится значение потенциальной энергии электрона на n-уровне:

,

а в левой части – удвоенное значение кинетической энергии электрона на том же уровне.

Другими словами, на любом энергетическом уровне потенциальная энергия превышает по абсолютной величине кинетическую энергию электрона в два раза. Полная энергия электрона равна:

Это полностью согласуется с излучательными переходами атома водорода.

Еще один важный вывод следует из приведенных выше соотношений. Квант действия h_n увеличивается в n раз с увеличением номера уровня, что и отражено в равенстве (2):

.

С учетом этого, длина волны де Бройля на n-орбите составляет:

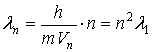,                                            (5)

где l₁ = 2pr₁ -длина волны де Бройля на первой боровской орбите.

Абсолютно постоянной величиной для любого стационарного состояния атома является т.н. стационарный поток напряженности G-поля через поверхность полусферы. Это следует из теоремы Остроградского-Гаусса для G-поля:

.                                (6)

Можно показать, что гравитационный поток Ф₀ выражается через длину волны де Бройля (5) и гравитационный потенциал орбиты так:

и на любом стационарном уровне атома остается константным.

При переходе атома из одного стационарного состояния в другое, в атоме возникает нестационарный процесс, который характеризуется вихревым GR-полем. При этом мгновенные значения физических величин существенно отличаются от своих значений в стационарном поле атома.

Для описания нестационарного процесса в атоме водорода используется наглядное средство – графика. Основанием для описания служит чакра ауры человека.

На рис. 1 приведена траектория движения электрона в пространстве при переходе с первой боровской орбиты на n-орбиту. В центре 0 системы координат находится ядро атома водорода. В плоскости ХOY расположены две стационарные круговые орбиты: внутренняя, исходная орбита 1 и внешняя, конечная, n-орбита. На время квантового перехода электрона обе орбиты фиксированы. Над орбитами изображены две полусферы соответствующих радиусов:   r₁   и   r_n.

Нестационарный процесс GR-поля атома условно разделен на три этапа, связанных с изменениями траектории движения электрона. В исходном состоянии электрон движется по круговой первой боровской орбите 1.

Первый этап – подъем электрона со стационарной орбиты 1 к полюсу полусферы 1. Он начинается с момента поглощения атомом кванта света, направление распространения которого показано стрелкой и совпадает с осью OZ. При этом электрон испытывает ускорение вдоль оси OZ, плавно сходит с орбиты 1 и по геодезической кривой поднимается в направлении полюса полусферы 1. Модуль радиуса-вектора r, проведенного из центра 0 к электрону e на первом этапе не изменяется, но его проекция на плоскость XOY с каждым витком локсодромы уменьшается и, наконец, достигает некоторого значения r_1-n, связанного с энергией поглощенного кванта света. Дальнейшее уменьшение этой проекции прекращается, подъем электрона закончен.

Второй этап – переход электрона с полусферы 1 на полусферу n. Траектория движения электрона перемещается на поверхность конуса, вершина которого находится в начале координат. Пересечение конуса с внутренней полусферой изображено на рис. 1 в виде окружности радиуса r_1-n, а с поверхностью внешней полусферы – окружностью радиуса r_n-n. По винтовой расходящейся спирали электрон достигает полусферы n. При этом проекция его радиуса-вектора увеличивается и достигает значения r_n-n.

Третий этап – снижение электрона на n-орбиту. Этот отрезок нестационарного процесса обратен первому, поэтому киральности спиралей геодезических кривых полусфер 1 и n различны. Радиус-вектор электрона, вращаясь вокруг оси OZ плавно опускается на плоскость XOY, а сам электрон – на стационарную n-орбиту. Квантовый переход электрона на n-уровень завершен, атом возвращается в стационарное состояние.

Энергетический уровень n-орбиты выше основного уровня и работа, затраченная GR-полем атома на подъем электрона, равна энергии поглощенного кванта света. В процессе обратного перехода электрона эта же энергия выделяется в виде излучения.

Процесс обратного перехода электрона, а также переходы между двумя любыми энергетическими уровнями атома характеризуются описанными этапами перехода и рис. 1.

Для выяснения соотношений между физическими величинами, характеризующими нестационарный процесс GR-поля атома водорода, рассмотрим схему квантового перехода, приведенную на рис. 2. Она соответствует переходу с энергетического уровня n == 1 на уровень n == 2, однако позволяет сделать обобщения для любого уровня.

На плоскости XOZ рис. 2. изображены кривые 1 и 2 пересечения полусфер 1 и 2 с плоскостью чертежа. На кривой 1 расположены характерные точки 1-1, 1-2, 1-3, …, 1-137, в которых геодезическая кривая полусферы 1 пересекает плоскость XOZ. Соответственно геодезическая кривая полусферы 2 пересекает плоскость чертежа в характерных точках кривой 2: 2-1, 2-2, 2-3, …, 2-137. Из центра 0 через характерные точки проведены прямые – образующие конусов соответствующих переходов.

Исходное положение электрона (движение по круговой орбите радиуса r₁) соответствует точке 1-1 схемы. С началом квантового перехода на уровень n == 2, электрон перемещается по кривой 1 в точку 1-2, затем по образующей конуса – в точку 2-2 кривой 2 и опускается по этой кривой в точку 2-1. Последняя соответствует движению электрона по круговой орбите радиуса r₂.

Проекции характерных точек кривой 1 на ось 0Х соответствуют радиусам  r_1-1, r_1-2, r_1-3,…, r_1-137; последние связаны с радиусом r₁ боровской орбиты так:

,                                                     (7)

где n = 1, 2, 3, …,137. Эти радиусы определяют длину волны де Бройля в характерных точках кривой 1:

.                                              (8)

Скорость движения электрона при подъеме с боровской орбиты плавно меняется, также как и длина волны. Но в точках 1-2, 1-3, … кривой 1 она принимает мгновенные значения, определенные формулой де Бройля:

(Здесь квант действия h_n = h т.к. п=1). С учетом соотношений (7) и (8) скорость электрона в точке n кривой 1 равна:

,

где V₁ - скорость движения электрона на первой  боровской орбите, n – номер уровня, на который осуществляется квантовый переход.

Если позволяет энергия поглощенного кванта, электрон может подняться по кривой 1 в точку 1-137, где скорость движения электрона достигает предельной скорости света с₀:

.

Это обстоятельство ограничивает не только минимально возможный радиус геодезической кривой значением радиуса Комптона:

,

но и количество максимально возможных энергетических уровней атома водорода n £ 137.

Примером нестационарного процесса в атоме служит эффект Комптона. При внешнем воздействии на электрон, находящийся на стационарной орбите, он обнаруживает длину волны Комптона:

.

В описываемой модели атома это соответствует подъему электрона по локсодроме в точку 1-137, в которой радиус окружности равен комптоновскому

,

а скорость равна скорости света с₀. С такой начальной скоростью электрон движется по спирали конуса Комптона и, либо переходит на 137-й энергетический уровень, либо уходит на бесконечность. Это зависит от энергии, сообщенной электрону.

Другим свидетельством нестационарного процесса в атоме является т.н. постоянная электромагнитного взаимодействия, которая в светодинамике имеет вид:

.

Это выражение для константы связи можно записать так:

.                                        (9)

Здесь делитель представляет собой поток напряженности G-поля атома через поверхность полусферы в стационарном состоянии (6). Можно показать, что делимое в равенстве (9) выражает поток G-поля в конусе Комптона:

.

Другими словами, константа связи электромагнитного взаимодействия устанавливает соотношение между G-потоком атома в конусе Комптона и G-потоком стационарного атома через полусферу:

.

В общем случае величина потока напряженности G-поля во время нестационарного процесса зависит от степени возбуждения атома:

,        (п = 1, 2, 3, …, 137).

Таким образом, при нестационарном процессе в атоме водорода наблюдается явление чакры, состоящее в n-кратном увеличении гравитационного потока ядра атома, сконцентрированного в узком конусе силового вихря.

Интересно отметить, что по геометрическим соотношениям конуса чакры возможно не только установление номера квантового перехода, но и длины излучаемой при этом волны, что очень важно при изучении аурического поля человека.

 

г. Сочи 2001г.